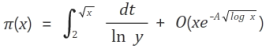Prime Factorization

In the post “Sieve of Eratosthenes“, I had posted a Java program for the prime sieve. Translating it to Python, I have:

from math import sqrt

def prime_sieve(limit) :
    crosslimit = int(sqrt(limit))
    sieve = [False]*limit

    for n in range(4, limit, 2) :
        sieve[n] = True
    for n in range(3, crosslimit+1, 2) :
        if not sieve[n]:
            for m in range(n*n, limit, 2*n) :
                sieve[m] = True

    num_primes = 0
    primes = []
    for n in range(2, limit) :
        if not sieve[n]:
            num_primes += 1

    for n in range(2, limit) :
        if not sieve[n]:
            primes.append(n)

    return primes

The list of primes generated by this sieve could then be used for factorizing a given number. For calculating the factors, I use the Trial Division algorithm, which isn’t the fastest, but easily implemented and not probabilistic. The algorithm basically tests if a given number (integer) n is divisible by any integer between 1 and n. Since only the prime factors of n are needed, we can use the list of primes generated from the sieve as a base set for the calculation, instead of the set of integers. Furthermore, the trial factors need go no further than  because, if n is divisible by some number p, then n = p×q and if q were smaller than p, n would have earlier been detected as being divisible by q or a prime factor of q.

A function in Python for prime factorization is:

def trial_division(n) :
    if n == 1: return [1]
    primes = prime_sieve(int(n**0.5) + 1)
    prime_factors = []

    for p in primes:
        if p*p > n: break
        while n % p == 0:
            prime_factors.append(p)
            n //= p
    if n > 1: prime_factors.append(n)

    return prime_factors

This method can be used for primality testing as well. If only one integer is returned by the method above (it would be same as the input number), then the input integer is a prime number. If the number of trial divisions required for an integer x is represented by π(x), then

for some A>0. The reason I chose to implement this algorithm in Python is that it follows Arbitrary-Precision Arithmetic. It runs satisfactorily well even for large numbers and doesn’t use a large amount of memory. In fact, if the overhead of generating the prime sieve is ignored, it becomes quite fast.

Sieve of Eratosthenes

The Sieve of Eratosthenes, named after the Greek mathematician Eratosthenes, is one of many known prime number sieves. The algorithm is a fairly good one for finding prime numbers from a list of numbers, say, less than 10 million.

Suppose we need to find all prime numbers below a natural number n > 1. Then, the algorithm is given as:

1. Create a list of consecutive integers from 2 to n: (2, 3, 4, …, n).
2. Initially, let p equal 2, the first prime number.
3. Starting from p, count up in increments of p, as long as the value is less than √n and mark each of these numbers greater than p itself in the list. These numbers will be 2p, 3p, 4p, etc.; note that some of them may have already been marked.
4. Find the first number greater than p in the list that is not marked; let p now equal this number (which is the next prime).
5. If there were no more unmarked numbers in the list, stop. Otherwise, repeat from step 3.

When, the above algorithm terminates, all unmarked numbers are prime.

The algorithm’s working is explained easily through the following image:

There are several variations to this algorithm. One says to initially list only odd numbers less than or equal to n. and count up using an increment of 2p in step 3, thus marking only odd multiples of p greater than p itself. Another, called the incremental sieve, is where prime numbers are generated indefinitely, without an upper bound.

The basic algorithm can be modified a bit for optimization. We only need to start crossing out multiples at p² , because any smaller multiple of p has a prime divisor less than p and has already been crossed out as a multiple of that. This is evident in the image above.

A simple implementation of this prime sieve algorithm is given below (Java)

class SieveOfEratosthenes
{
	static int[] Sieve(int limit)
	{
		int crosslimit = (int)Math.sqrt(limit);
		boolean[] sieve = new boolean[limit];
		int m, n;

		for(n = 4; n < limit; n += 2)
			sieve[n] = true;

		for(n = 3; n < crosslimit; n +=2)
			if(!sieve[n])
				for(m = n*n; m < limit; m += 2*n)
					sieve[m] = true;

		int num_primes = 0;
		for(n = 2; n < limit; n++)
			if(!sieve[n])
				num_primes++;

		int[] primes = new int[num_primes];
		int i = 0;
		for(n = 2; n < limit; n++)
			if(!sieve[n])
				primes[i++] = n;

		return primes;
	}

	public static void main(String args[])
	{
		int l = 1000;
		int[] p = Sieve(l);
		for(int i=0; i < p.length; i++)
			System.out.println(p[i]);
	}
}

Analysis:

In the program above, the Sieve of Eratosthenes algorithm is implemented in the method Sieve(). It takes an integer, limit, as argument. This is the bound below which all prime numbers are to be found. Being an integer, the maximum value that it can hold is 2,147,483,647. The Sieve() method returns an integer array containing all prime numbers below limit in ascending order.

For the list of numbers, we use a boolean array sieve of length limit, indicating which numbers are composite. If sieve[x] is true, then it means x is a composite number. The limit for checking for primality, or as in this case, non-primality, is √limit. This is saved in the integer variable crosslimit. In the first for loop, ranging from 4 to limit, we set all even indices to true. Thus, 2 is considered prime, and all other even numbers have been crossed out. The rest of the algorithm lies in the second for loop.

Starting from 3, and progressing for odd numbers, we find their multiples and cross them out. The multiples of a number n are crossed out beginning at n² and ending at limit – 1, progressing at a step size of 2n (as we need only consider odd multiples). All multiples of p less than p² will already have been crossed out as multiples of smaller prime numbers. This step is not required for odd composites as they and their multiples have already been crossed out. This is achieved using the if(!sieve[n]) statement, where the inner for loop does not execute if sieve[n] is true, i.e. n is composite.

The next few lines are used to count the number of primes less than limit by counting the number of false values in the array sieve[]. Next we create an integer array primes, with the size as number of primes found, holding all the prime numbers from 2 to limit. This array is then returned to main(). In the main method, we store the bound in the integer variable l and the prime numbers are returned to the array p. At the end, we print each of the primes by traversing through the array with a for loop.